NUS Soc SWS3005 实时 3D 图形渲染

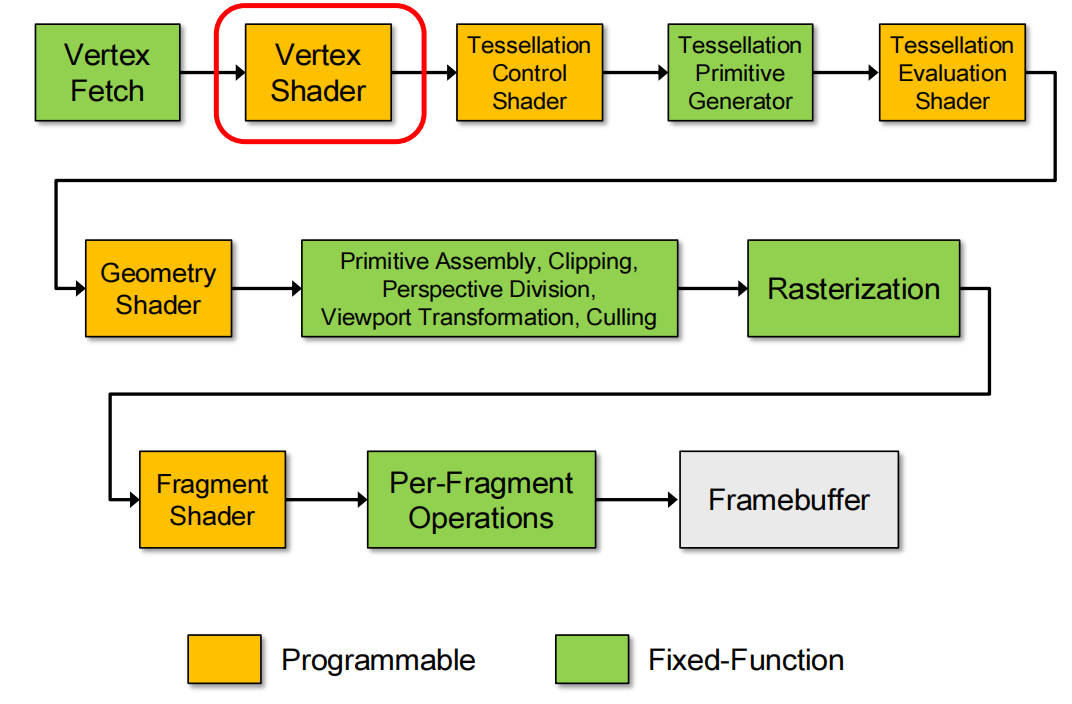
I. Pre-Knowledge (Phase 1)

Image Formation

How does a realistic graphic form?

Elements of Image Formation

• Objects
• Viewer
• Light sources
• Materials (材质)
  • Attributes that govern how light interacts with the materials in the scene

Models

Know about Pinhole Camera

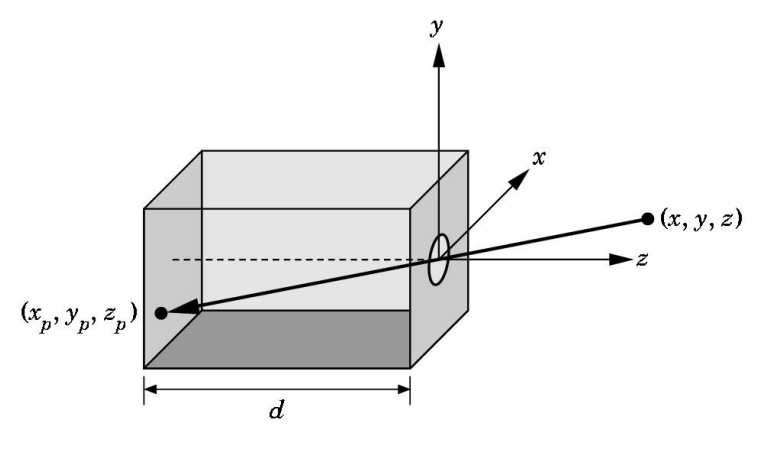
Use trigonometry(三角几何) to find projection of 3D point at $(x, y, z)$

$
x_p=-dx/z\ \ \ \ y_p=-dy/z\ \ \ \ z_p=-d
$

Synthetic Camera Model (合成相机模型)

Luminance and Color Images (光线与颜色的映射)

• Luminance Image
  • Monochromatic(单色)
    • Values are gray levels
    • Analogous to working with black and white film or television
• Color Image
  • Has perceptional attributes of hue(色相), saturation(饱和度), and lightness

↓

• Representation of Color
  • Additive color: Form a color by adding amounts of three primaries(RGB)
    • E.g. CRTs, projection systems, positive film
  • Subtractive color: Form a color by filtering white light with Cyan (C), Magenta (M), and Yellow (Y) filters
    • Noted: Cyan = –Red; Magenta = –Green; Yellow = –Blue

---

Graphics System Design

A graphics system has two main components

1. Application Programmer Interface (API)
   • For specifying the scene
     • objects, materials, viewer, lights
   • For configuring/controlling the system
2. Renderer
   • Renders the images
     • Using scene info and system configuration

Rendering Approaches

1. Ray tracing: follow rays of light from center of projection until they are absorbed by objects or go off to infinity
   • 符合物理解释，泛用性广；但是速度慢，性能低
2. Radiosity: Energy based approach
   • 非常慢且不泛用

Practical Approach

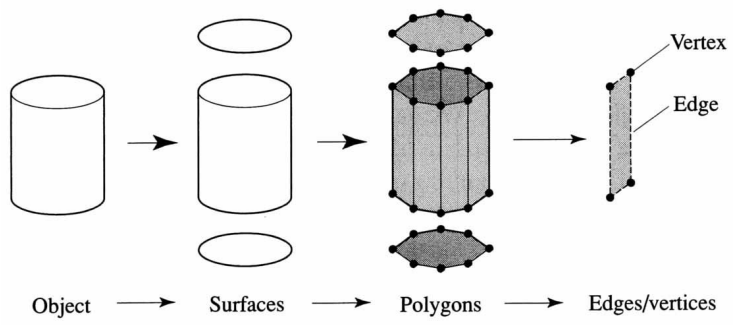
1. Polygon Rasterization(多边形光栅)

3D 物体可以近似地表示为平面多边形刻面 (planar polygonal facets) 的网或网格

Pipeline architecture

The pipeline consists of stages that each primitive (e.g. polygon) must go through

Vertices -> |Vertex processor| -> |Clipper and primitive assembler| -> |Rasterizer| 
-> |Fragment processor| -> Pixels

(i) Vertex Processing

• Much of the work in the pipeline is in converting object representations from one coordinate system to another
  • Object coordinates
  • Camera (eye) coordinates
  • Screen coordinates
• Also computes vertex colors

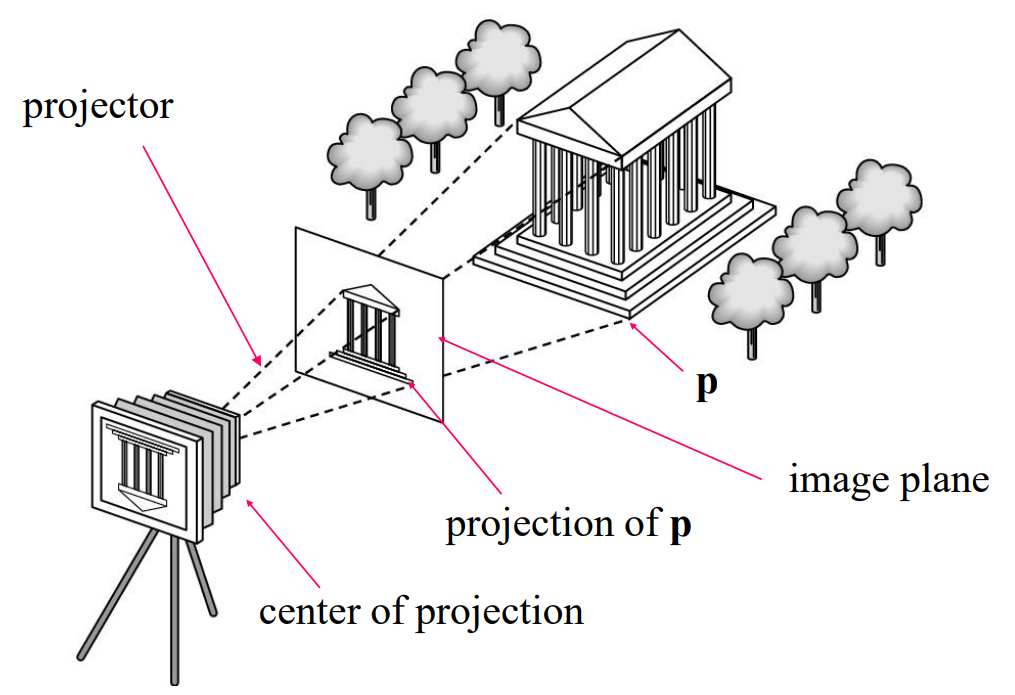
(ii) Projection

• Projection is the process that combines the 3D viewer with the 3D objects to produce the 2D image
  • Perspective projections: all projectors meet at the center of projection
  • Parallel projection: projectors are parallel, center of projection is replaced by a direction of projection

(iii) Clipping

• Simulate a virtual camera to clip the images

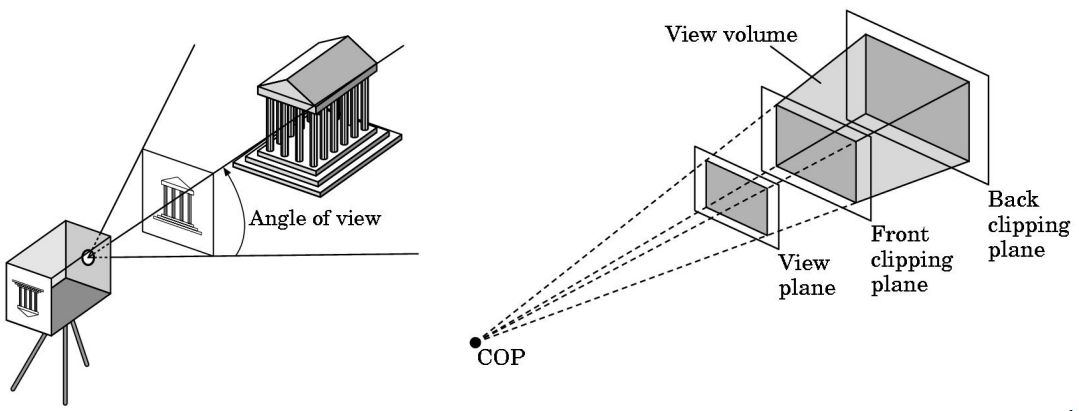
(iv) Rasterization

• Rasterizer produces a set of fragments for each object
• Fragments are “potential pixels”
  • Have a location in frame bufffer
  • Color and depth attributes

Fragment Processing

• Fragments are processed to determine the color of the corresponding pixel in the frame buffer
• Colors can be determined by texture mapping or interpolation(插值) of vertex colors
• Fragments may be blocked/occluded(阻塞) by other fragments closer to the camera
  • Using Hidden-surface removal

---

API Contents

• Recall: Functions that specify what we need to form an image
  • Objects
  • Viewer
  • Light Source(s)
  • Materials

Object Specifications

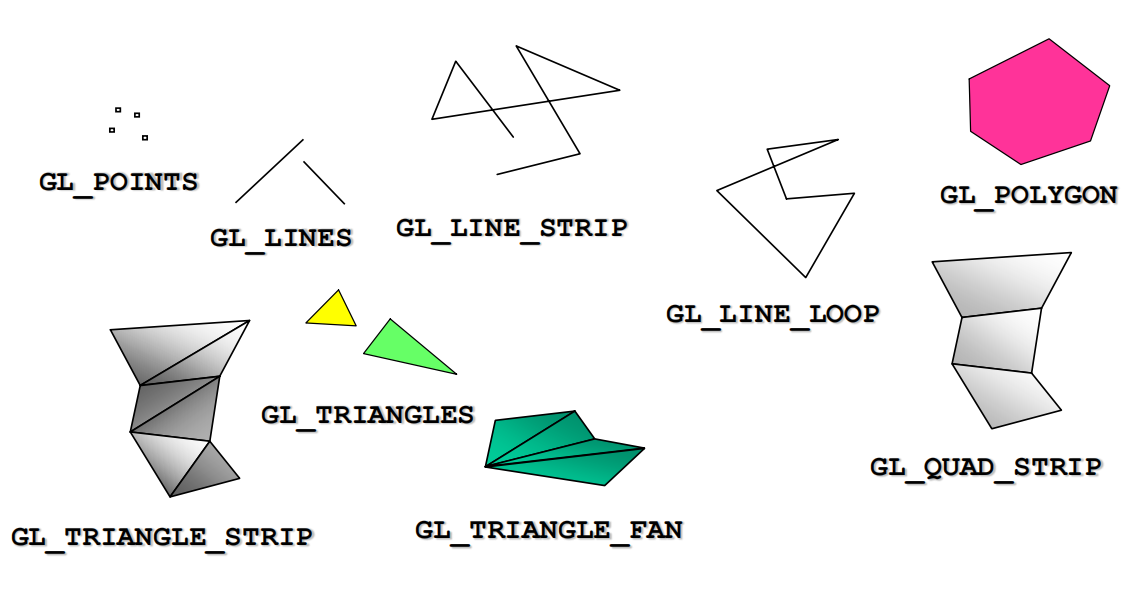
• Most APIs support a limited set of primitives including
  • Points (0D object)
  • Line segments (1D objects)
  • Polygons (2D objects)
  • Some curves and surfaces
    • Quadrics
    • Parametric polynomials
• All are defined through locations in space or vertices

Camera Specification

• Six degrees of freedom
  • Position of center of lens
  • Orientation
• Lens
• Film size
• Orientation of film plane

Lights and Materials

• Types of lights
  • Point sources vs distributed sources
  • Spot lights
  • Near and far sources
  • Color properties
• Material properties
  • Absorption: color properties
  • Scattering
    • Diffuse
    • Specular

----- Let's start Phase 2! -----

II. Elementary OpenGL Programming

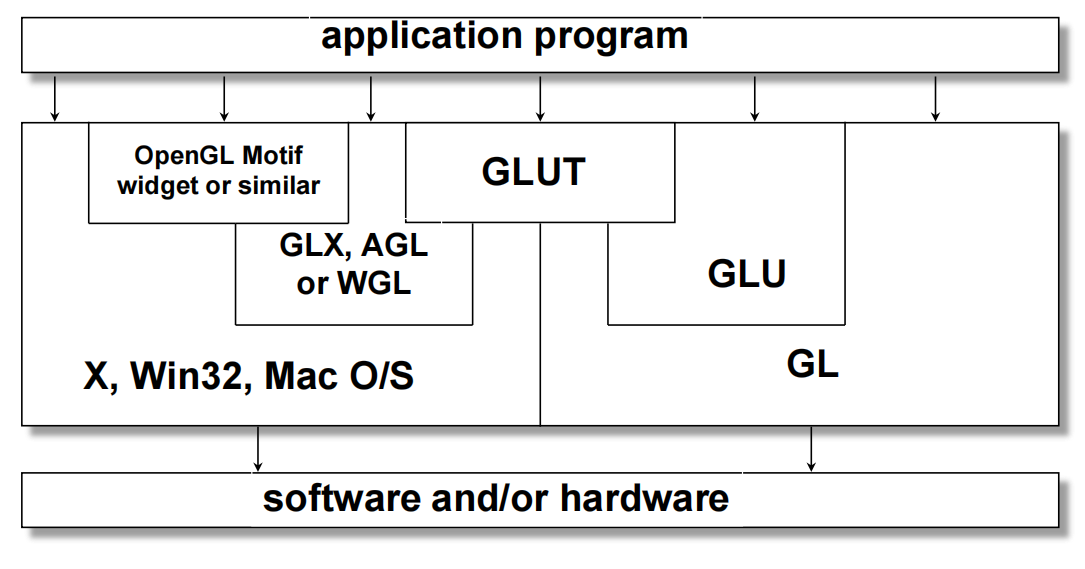
OpenGL Libraries

Core Library

• OpenGL core library
  • OpenGL32 on Windows
  • GL on most unix/linux systems ( libGL.a )
• OpenGL Utility Library ( GLU )
  • Provides functionality in OpenGL core but avoids having to rewrite code
• Links with window system
  • GLX for X window systems
  • WGL for Windows
  • AGL for Macintosh

GLUT / FreeGLUT Libraries

• GLUT = OpenGL Utility Toolkit
  • Not part of OpenGL
  • Provides functionality common to all window systems
    • Open a window
    • Get input from mouse and keyboard
    • Menus
    • Event-driven
  • Code is portable but GLUT lacks the functionality of a good toolkit for a specific platform
    • No slide bars
• FreeGLUT

Software Organization

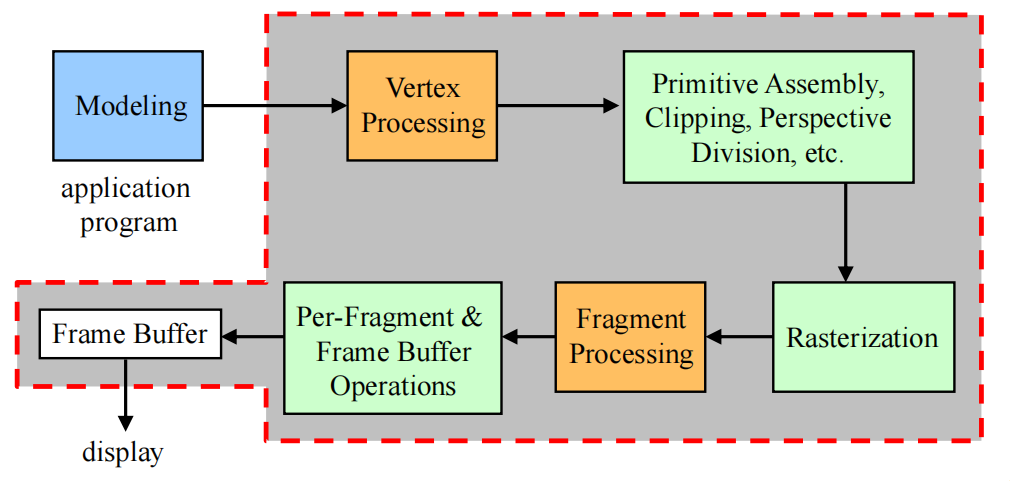
Basic OpenGL Rendering Pipeline

• To render a primitive using OpenGL, the primitive goes through the following main stages:
  • Goal: Turning primitive into pixels

OpenGL Functions

• Specify primitives
  • E.g. points, line segments, triangles, quadrilaterals, polygons
• Specify vertex attributes
  • E.g. color, normal vector, material, texture coordinates
• Specify transformations
  • E.g. modeling, viewing
• Control (GLUT)
• Input (GLUT)
• Query: “ask for the state of object” etc.

OpenGL State

• OpenGL is a state machine

• OpenGL functions are of two types

  • Primitive generating
    • Can cause output if primitive is visible
    • How vertices are processed and appearance of primitive are controlled by the state
  • State changing
    • Transformation functions
    • Attribute functions

Simple Concept

Examples

#include <GL/glut.h>
void mydisplay() {
    glClear(GL_COLOR_BUFFER_BIT); 
    glBegin(GL_POLYGON); 
    glVertex2f(-0.5, -0.5); 
    glVertex2f(-0.5, 0.5); 
    glVertex2f(0.5, 0.5); 
    glVertex2f(0.5, -0.5); 
    glEnd();
    glFlush(); 
}
int main(int argc, char** argv) {
    glutInit(&argc, argv);
    glutCreateWindow("simple"); 
    glutDisplayFunc(mydisplay); 
    glutMainLoop();
}

This code is to draw a white square in black background.

Event Loop

Note that the program defines a display callback function named mydisplay

• Every GLUT program must have a display callback
• The display callback is executed whenever OpenGL decides the display must be refreshed
  • For example, when the window is opened
• The main function ends with the program entering an event loop

Program Structure

• Most OpenGL programs have a similar structure that consists of the following functions
  • main():
    • defines the callback functions
    • opens one or more windows with the required properties
    • enters event loop (last executable statement)
  • init(): sets the state variables
    • Viewing
    • Attributes
  • callbacks
    • Display callback function
    • Input and window functions

Then we’re going to see an explicit form of Example

main()

#include <GL/glut.h>
int main(int argc, char** argv)
{
	glutInit(&argc, argv); 
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 
	glutInitWindowSize(500, 500); 
	glutInitWindowPosition(0, 0); 
	glutCreateWindow("simple2"); 
	glutDisplayFunc(mydisplay); 
	init(); 
	glutMainLoop();
}

• glutInit —— allows application to get command line arguments and initializes system
• gluInitDisplayMode —— requests properties for the window (the rendering context)
  • RGB color
  • Single buffering
  • Properties logically ORed together
• glutWindowSize —— in pixels
• glutWindowPosition —— from top-left corner of display
• glutCreateWindow —— create window with title “simple”
• glutDisplayFunc —— display callback
• glutMainLoop —— enter infinite event loop

init()

void init()
{
	glClearColor(0.0, 0.0, 0.0, 1.0); 
	// black clear color with opaque window
	glColor3f(1.0, 1.0, 1.0); // white fill color
	glMatrixMode(GL_PROJECTION); 
	glLoadIdentity(); 
	glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0); // viewing volume
}

• Coordinate Systems (have a rough knowing)
  • object coordinates (3D)
  • world coordinates (camera)
  • window coordinates
• About OpenGL Camera

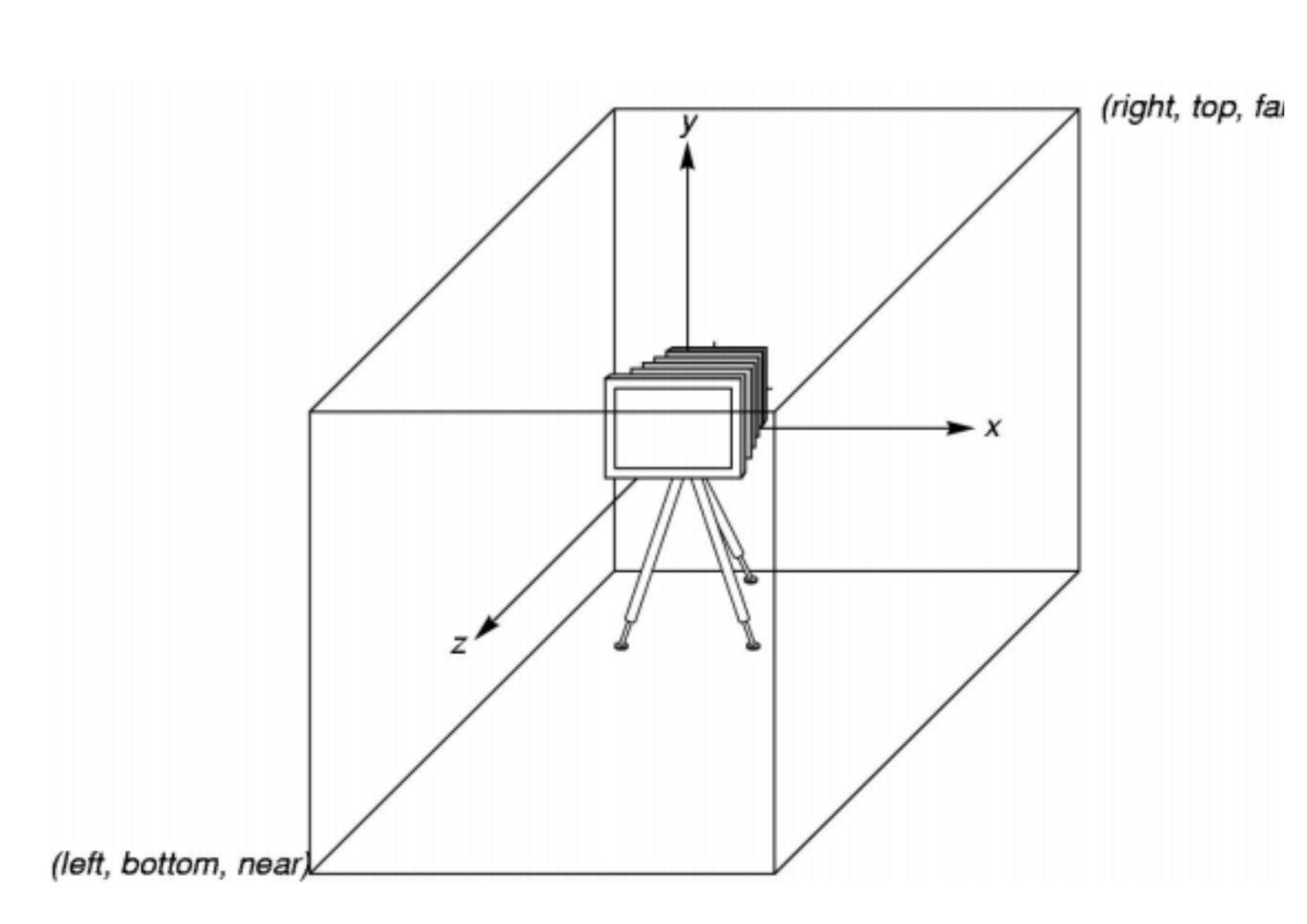
• Orthographic Viewing and Transformation
  • In the default orthographic view, points are projected forward along the $z$ axis onto the plane $z = 0$
  • In OpenGL, projection is carried out by a projection matrix (transformation)
  • There is only one set of transformation functions so we must set the matrix mode first
    • glMatrixMode(GL_PROJECTION)
  • Transformation functions are incremental so we start with an identity matrix and alter it with a projection matrix that gives the view volume
    • glLoadIdentity();
    • glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0);
  • glOrtho(left, right, bottom, top, near, far) is used to determine the projection area.
  • If the application is in 2D, we can use the function gluOrtho2D(left, right, bottom, top)

Here is an example of how to draw a projection on 2D windows.

Because a projection from 3D to 2D is in OpenGL-Primitives (I show below), so we only need to paint it out.

void mydisplay()
{
	glClear(GL_COLOR_BUFFER_BIT); 
	glBegin(GL_POLYGON); 
	// define as polygon
	glVertex2f(-0.5, -0.5); 
	glVertex2f(-0.5, 0.5); 
	glVertex2f(0.5, 0.5); 
	glVertex2f(0.5, -0.5); 
	// set 4 vertex to form 4-edges polygon
	glEnd();
	glFlush(); 
}

Other methods of OpenGL

1. glShadeModel() to set the color rendering to be GL_SMOOTH (渐变) or GL_FLAT (单色).
2. glViewport(x, y, w, h) to set the viewport of windows.

3D OpenGL

Three-Dimensional Applications

• In OpenGL, 2D applications are a special case of 3D graphics
• Going to 3D
  • Not much changes
  • Use glVertex3*()
  • Have to worry about the order in which polygons are drawn or use hidden-surface removal (occlusion problem)
  • Polygons should be simple, convex, flat

Gasket Program

• Consider the filled area (black) and the perimeter (the length of all the lines around the filled triangles)
• As we continue subdividing
  • the area goes to zero (< 2D)
  • but the perimeter goes to infinity (> 1D)
• This is not an ordinary geometric object
  • It is neither one- nor two-dimensional
• It is a fractal (fractional dimension) object
  • Approximately 1.585 D

How to do in program? Using algorithm of Recursion!

• Design display() and myinit()

void display()
{
    glClear(GL_COLOR_BUFFER_BIT);
    glBegin(GL_TRIANGLES);
    divide_triangle(v[0], v[1], v[2], n);
    glEnd();
    glFlush();
}

void myinit()
{
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluOrtho2D(-2.0, 2.0, -2.0, 2.0);
    glMatrixMode(GL_MODELVIEW);
    glClearColor (1.0, 1.0, 1.0, 1.0);
    glColor3f(0.0,0.0,0.0);
}

• Then set parameter and callback function in main()

int main(int argc, char **argv)
{
    n = 4;
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    glutInitWindowSize(500, 500);
    glutCreateWindow("Sierpinski Gasket");
    glutDisplayFunc(display);
    myinit();
    glutMainLoop();
}

---

Move to 3D triangle

• Add an extra vertex to form tetrahedra
• Then we can do like 2D triangle subdivision

But we have to deal with Hidden-Surface Removal !!

• • OpenGL uses a hidden-surface removal method called the z-buffer algorithm that saves depth information as objects are rendered so that only the front objects appear in the image.

Using the z-buffer Algorithm

Requested in main()

glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH)

Enabled in init()

glEnable(GL_DEPTH_TEST)

Cleared in the display callback

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)

Surface vs. Volume Subdivision

• In our example, we subdivided the surface of each face
• We could also subdivide the volume using the same midpoints
• The midpoints define four smaller tetrahedrons, one for each vertex
• Keeping only these tetrahedrons removes a volume in the middle
• Good programming exercise

---

III. Input & Interaction

Concept

• Graphical Input
  • Devices can be described either by
    • Physical properties
      • Mouse, Keyboard, Trackball, etc.
    • Logical properties: What is returned to program via API
      • A position
      • An object identifier

• Trigger and Measure

  • Input devices contain a trigger which can be used to send a signal to the operating system
    • Button on mouse
    • Pressing or releasing a key
  • When triggered, input devices return information (their measure) to the system
    • Mouse returns position information
    • Keyboard returns ASCII code

• Event Mode

  • Each trigger generates an event whose measure is put in an event queue which can be examined by the user program

• Event Type

  • Window: resize, expose, minimize
  • Mouse: click one or more buttons
  • Motion: move mouse
  • Keyboard: press or release a key
  • Idle: non-event (无输入时的活动)
    • Define what should be done if no other event is in queue

• Recall: callbacks

  • Define a callback function for each type of event the graphics system recognizes
  • E.g. glutMouseFunc(mymouse) where mymouse is a mouse callback function.
• GLUT recognizes a subset of the events recognized by any particular operation system :
  • glutDisplayFunc
  • glutMouseFunc
  • glutReshapeFunc
  • glutKeyboardFunc
  • glutIdleFunc
  • glutMotionFunc, glutPassiveMotionFunc

GLUT Event Loop

• Recall: the last statement in main() for a program using GLUT must be glutMainLoop();
• In each pass through the event loop, GLUT
  • looks at the events in the queue
  • execute each event if the corresponding callback function is defined.

Important before talking about callbacks:

• The form of all GLUT callbacks is fixed
• So we must use globals (全局变量) to pass information to callbacks

Display Callback

• When windows are refreshed, apply display callbacks
  • glutDisplayFunc(mydisplay) in main()
  • glutPostRedisplay() to avoid multiple display in one single pass through the event loop
    • set a “flag” at the end of the event loop.
    • GLUT checks it and display callback function is executed.
• Then what’s inside mydisplay?
  • glClear() to clear the window
  • Use Double Buffer to avoid partial drawn
    • Front Buffer: one that is displayed but not written to
    • Back Buffer: one that is written to but not displayed
  • glutInitDisplayMode(GLUT_RGB | GLUT_DOUBLE) declare in main() to request a double buffer
  • At the end of display callback buffers are swapped.

void mydisplay()
{
 glClear(GL_COLOR_BUFFER_BIT|…)
 ...
 /* draw graphics here */
 ...
 glutSwapBuffers();
}

Idle Callback

• The idle callback is executed whenever there are no events in the event queue
  • glutIdleFunc(myidle) in main()
  • Useful for animation

void myidle() {
 /* change something */
 t += dt
 glutPostRedisplay();
}

Mouse and Keyboard Callbacks

• glutMouseFunc(mymouse) in main()
• void mymouse(GLint button, GLint state, GLint x, GLint y) to define mouse callbacks
  • Buttons: GLUT_LEFT_BUTTON, GLUT_MIDDLE_BUTTON or GLUT_RIGHT_BUTTON
  • States: GLUT_UP or GLUT_DOWN
  • Cursor Position: top-left corner is (0,0) [Others depend on winsize]

$
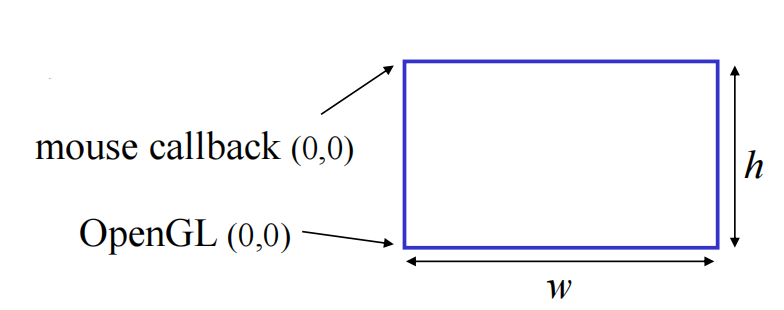
y_{\text{OpenGL}}= h-1-y_{text{win}}
$

E.g. To draw a square when mouse click

void mymouse(int btn, int state, int x, int y)
{
 if (btn==GLUT_RIGHT_BUTTON && state==GLUT_DOWN) exit(0);
 if (btn==GLUT_LEFT_BUTTON && state==GLUT_DOWN) drawSquare(x, y);
}
void drawSquare(int x, int y)
{
 y = w – 1 - y; /* invert y position */
 /* a random color */
 glColor3ub((char)rand()%256,(char)rand()%256,(char)rand()%256 );
 glBegin(GL_POLYGON);
 glVertex2f(x+size, y+size);
 glVertex2f(x-size, y+size);
 glVertex2f(x-size, y-size);
 glVertex2f(x+size, y-size);
 glEnd();
}

---

• We can draw squares (or anything else) continuously as long as a mouse button is depressed by using the motion callback
  • glutMotionFunc(drawSquare)

• We can draw squares without depressing a button using the passive motion callback (用于鼠标没按下但在移动时的操作)

  • glutPassiveMotionFunc(drawSquare)

• Keyboard is almost the same

  • glutKeyboardFunc(mykey)
  • void mykey(unsigned char key, int x, int y)

E.g.

void mykey(unsigned char key, int x, int y)
{
 if (key == 'Q' | key == 'q') 
 exit(0);
}

Others:

GLUT defines the special keys in glut.h

• Function key 1: GLUT_KEY_F1
• Up arrow key: GLUT_KEY_UP

Also check modifiers

• GLUT_ACTIVE_SHIFT, GLUT_ACTIVE_CTRL, GLUT_ACTIVE_ALT is depressed using glutGetModifiers()

Reshape Callback

• glutReshapeFunc(myreshape) in main()
• void myreshape(int w, int h)

E.g.

void myReshape(int w, int h)
{
 glViewport(0, 0, w, h);
 glMatrixMode(GL_PROJECTION); /* switch matrix mode */
 glLoadIdentity();
 
 if (w <= h)
 gluOrtho2D( -2.0, 2.0, -2.0 * (GLfloat) h / w,
 2.0 * (GLfloat) h / w );
 else 
 gluOrtho2D( -2.0 * (GLfloat) w / h, 
 2.0 * (GLfloat) w / h, -2.0, 2.0 );
 glMatrixMode(GL_MODELVIEW); /* return to modelview mode */
}

Menu

// main()
GLint menu_id = glutCreateMenu(mymenu);
glutAddMenuEntry("Clear", 1);
glutAddMenuEntry("Quit", 2);
glutAttachMenu(GLUT_RIGHT_BUTTON);

void mymenu(int id)
{
 if(id == 1) glClear(GL_COLOR_BUFFER_BIT);
 if(id == 2) exit(0);
}

Other Functions

• Dynamic Windows
  • Create and destroy during execution
• Subwindows
• Multiple Windows
• Changing callbacks during execution
• Timers (look up glutTimerFunc)
  • Useful for controlling speed of animation
• Portable fonts
  • glutBitmapCharacter
  • glutStrokeCharacter

---

IV. Geometric Objects & Transformations

• Basic elements
  • Scalars
  • Vectors
  • Points
• Basic primitives
  • Line segments
  • Polygons

Representation

• Introduce
  • coordinate systems for representing vector spaces
  • frames for representing affine spaces(仿射空间)
• Discuss change of frames and bases
• Introduce homogeneous coordinates

Coordinate Systems

Recall: Linear Algebra

• basis: $v_1,v_2,…,v_n$
• a vector written as $v=\alpha_1 v_1+\alpha_2 v_2 + \cdots + \alpha_n v_n$
• the coordinate of $v$ in this basis is $\{ \alpha_1,\alpha_2, \cdots , \alpha_n \}$

Frame

Def. A frame is a system with a single point(origin $P_0$) and a basis vector in an affine space.

$
P=P_0 + \beta_1 v_1 + \beta_2 v_2 + \cdots + \beta_n v_n
$

Homogeneous Coordinates

E.g. for a 3 * 3 space, the 3 * 3 matrices cannot used for translation(平移), because vectors have no position.

• We extend the $3\times 3$ point to 4-dimension: $(x,y,z) \rightarrow (x,y,z,1)$
• and a $4\times 4$ matrix can represent translation, rotation and scaling and shear
• using matrix(a template) below, we can maintain $w=0$ for vectors and $w=1$ for points for orthographic viewing .

$
\left( \begin{array}{c}
a & b & c & tx \\
d & e & f & ty \\
g & h & i & tz \\
0 & 0 & 0 & 1
\end{array}\right)
$

E.g. For a 3D point $(x,y,z)$ , its homogeneous coordinate is $P_h = (x,y,z,1)$ . To translate it, we define a matrix:

$
\left( \begin{array}{c}
1 & 0 & 0 & tx \\
0 & 1 & 0 & ty \\
0 & 0 & 1 & tz \\
0 & 0 & 0 & 1
\end{array}\right)
\left( \begin{array}{c}
x \\ y \\ z \\ 1
\end{array}\right) =
\left( \begin{array}{c}
x+ tx \\ y+ ty \\ z+ tz \\ 1
\end{array}\right)
$

• More generally, homogeneous coordinates are represented as $p=[ wx,wy,wz,w ]^T$

Transformation

• Affine Transformation: Line preserving

• Translation: move points

  • $P’=P+d$ where $d=[d_x, d_y, d_z, 0]^T$

• Recall for Linear Algebra: Some linear transformation:

  • Rotation (2D)
  • Scaling
  • Reflection

try to remember their transformation matrices.

Inverses

• Translation: $\textbf{T}^{-1}=\textbf{T}(-d_x, -d_y, -d_z)$
• Rotation: $\textbf{R}^{-1}(\theta)=\textbf{R}(- \theta)$
  • Noted that only $cos(\theta)$ on orthogonal entry
• Scaling: $\textbf{S}^{-1}(s_x, s_y, s_z)=\textbf{S}(1/s_x, 1/s_y, 1/s_z)$

Examples

Rotation About a Fixed Point Other than the Origin:

1. Move fixed point to origin
2. Rotate
3. Move fixed point back

$
\textbf{M}=\textbf{T}(p_f)\textbf{R}(\theta)\textbf{T}(-p_f)
$

(bu)

OpenGL Transformations

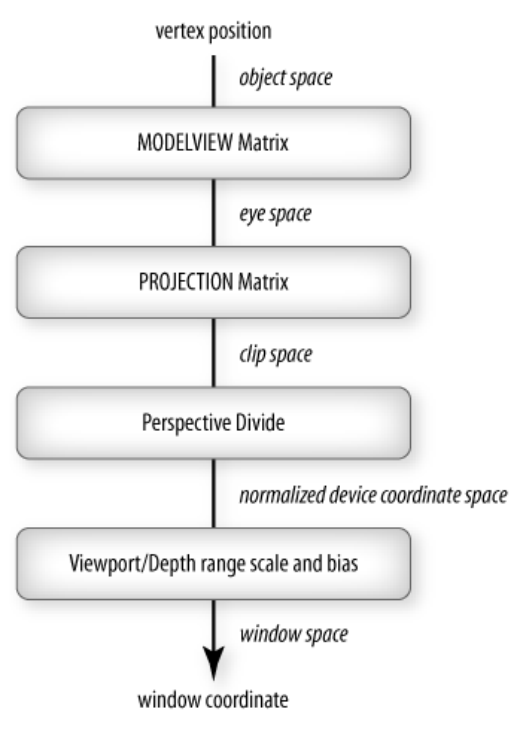
• Recall: glMatrixMode(GLenum mode) to change the mode of matrix calculation

  • when doing transformation, use GL_MODELVIEW state

• For all CTM(Current Transformation Matrix) Operations, our CPP Code must load identity matrix first:

glMatrixMode(GL_MODELVIEW);
glLoadIdentity(); // 重置
glTranslatef(0.0, 0.0, -5.0); // 平移物体

• Beware of using post-multiplications (the later operations should be multipled to result matrix $\textbf{C}$ earlier)
  • E.g. Rotation About a Fixed Point: $\textbf{C}=\textbf{T}^{-1}\textbf{R}\textbf{T}$
• Other Transformation Matrix specifying
  • rotation: glRotatef(theta, vx, vy, yz)
  • translation: glTranslatef(dx, dy, dz)
  • scale: glScalef(sx, sy, sz)

---

V. Camera & Viewing

Computer Viewing

• 2 attributes to define the viewing:
  • Positioning the camera
    • Setting the model-view matrix
  • Selecting a lens
    • Setting the projection matrix
    • Perspective or orthographic / view volume / clipping volume …

Specify Different Space

• Local / Modeling / Object Space
  • Each object model has its own local coordinate frame
• World Space (类似全局空间)
  • Lights and Camera pose are defined in this space

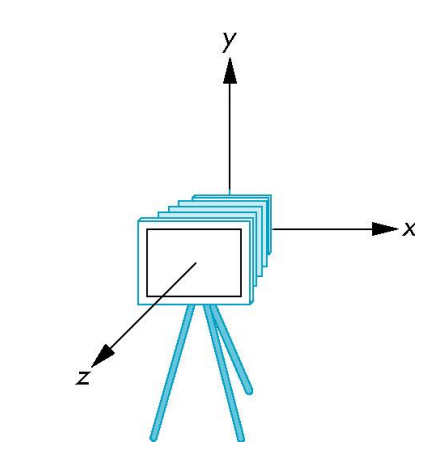
• Camera Space / View Space / Eye Space
  • Camera is located at the origin
  • Looking in negative $z$ direction
  • $+y$-axis is the “up-vector”

Initially the world and camera frames are the same.

To specify camera pose, we need to specify the camera coordinate frame with respect to the world coordinate frame.

View Transformation

glLookAt( eyex, eyey, eyez,
		  atx , aty , atz ,
		  upx , upy , upz )

• 通过 eye 和 at 求出前向量

$
\text{forward}=\frac{\text{at} - \text{eye}}{|\text{at} - \text{eye}|}
$

• 通过 forward 和 up 求出右向量

$
\text{side}=\frac{\text{forward} \times \text{up}}{|\text{forward} \times \text{up}|}
$

• 然后就能得到修正后的上向量

$
\text{up’}= \text{forward} \times \text{side}
$

• 求出三个向量后就能确定 camera 的位置和 pose 了

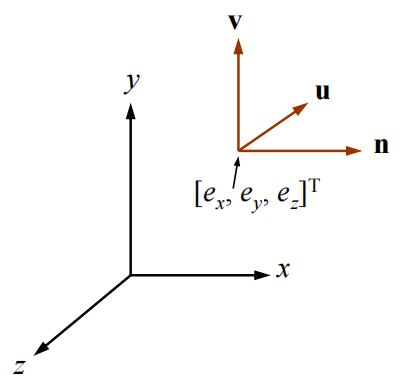
• Suppose the camera has been moved to the location $[e_x, e_y, e_z]^T$, and its $x_c$, $y_c$, $z_c$ axes are the unit vectors $\textbf{u}$, $\textbf{v}$, $\textbf{n}$, respectively, then

$
\textbf{M}_{\text{view}}=
\left[ \begin{array}{c}
u_x & u_y & u_z & 0 \\
v_x & v_y & v_z & 0 \\
n_x & n_y & n_z & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\cdot
\left[ \begin{array}{c}
1 & 0 & 0 & -e_x \\
0 & 1 & 0 & -e_y \\
0 & 0 & 1 & -e_z \\
0 & 0 & 0 & 1
\end{array}\right]
$

▪ Note that $[e_x, e_y, e_z]^T$ and $\textbf{u}$, $\textbf{v}$, $\textbf{n}$ are all specified with respect to the world frame

Projection —— Defining the View Volume

• For orthographic projection, use glOrtho()
• For perspective projection, use glFrustum()

OpenGL Orthographic Projection

• The glOrtho() function then generates a matrix that linearly maps the view volume to the canonical view volume, where
  • (left, bottom, –near) is mapped to (–1, –1, –1)
  • (right, top, – far) is mapped to (1, 1, 1)

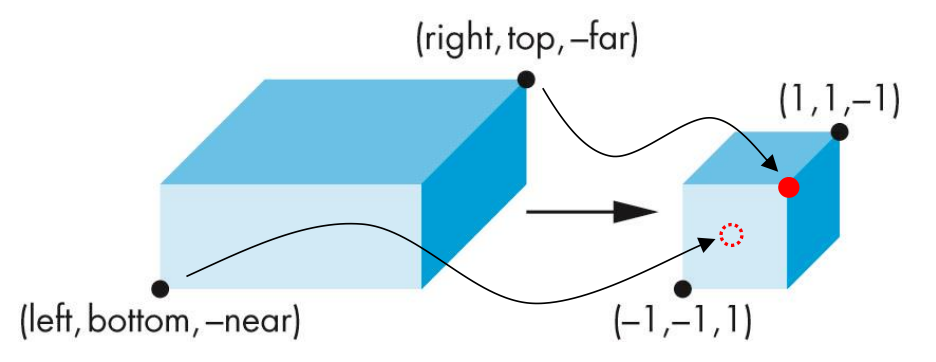
正投影，能较真实地反映物体大小，物体显示的大小不会因视角变化改变。常用于CAD设计、地图绘制、2D游戏等不需要表现深度感的场景。

OpenGL Perspective Projection

• glFrustum( left, right, bottom, top, near, far )
  • The glFrustum() function allows (off-center) non-symmetric view volume
• Often, we want a symmetric view volume. We can use
  • gluPerspective( fovy, aspect, near, far );

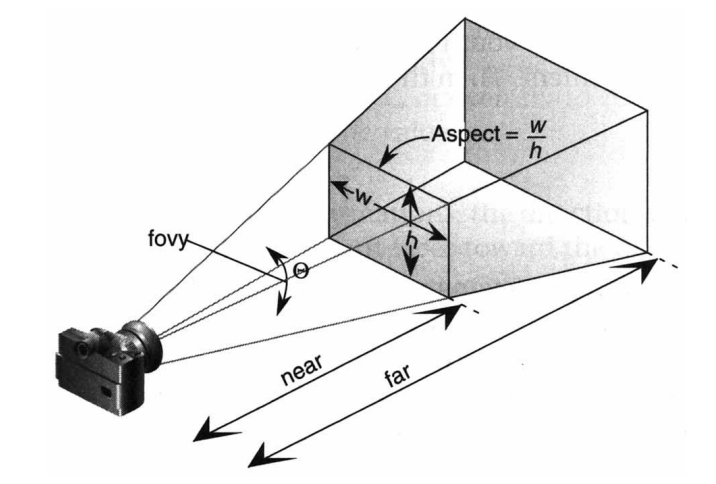
透视投影，有深度感，近大远小。常用于3D游戏、虚拟现实、建筑可视化等需要真实感的场景。

Principle of Perspective Projection

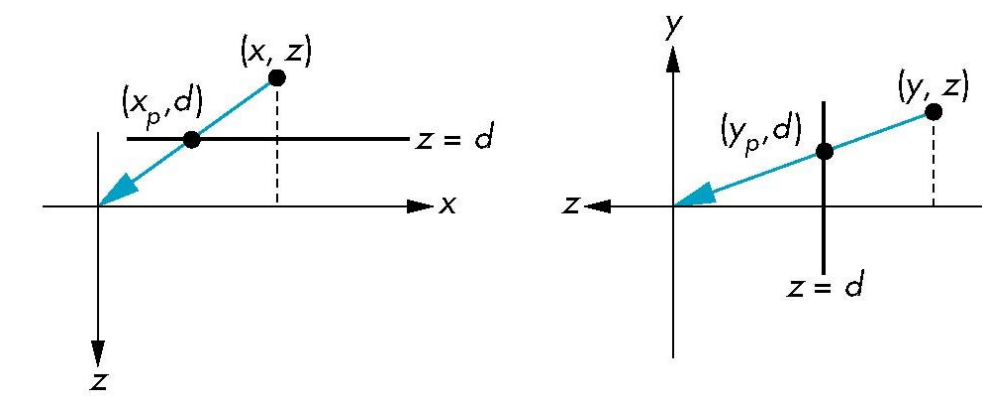
• Center of projection at the origin
• Projection plane is $z = d$, $d < 0$

$
x_p=\frac{x}{z/d}\ \ \ \ y_p=\frac{y}{z/d}\ \ \ \ z_p=d
$

• Consider $p=Mq$ where

$
p=
\left[ \begin{array}{c}
x \\ y \\ z \\ z/d
\end{array}\right] \ \ \ \ M=
\left[ \begin{array}{c}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 1/d & 0
\end{array}\right] \ \ \ \ q=
\left[ \begin{array}{c}
x \\ y \\ z \\ 1
\end{array}\right]
$

• If we scale $p$ , then we get the projection point on plane $z=d$ .

VI. Rasterization

Recall for OpenGL Rendering Pipeline

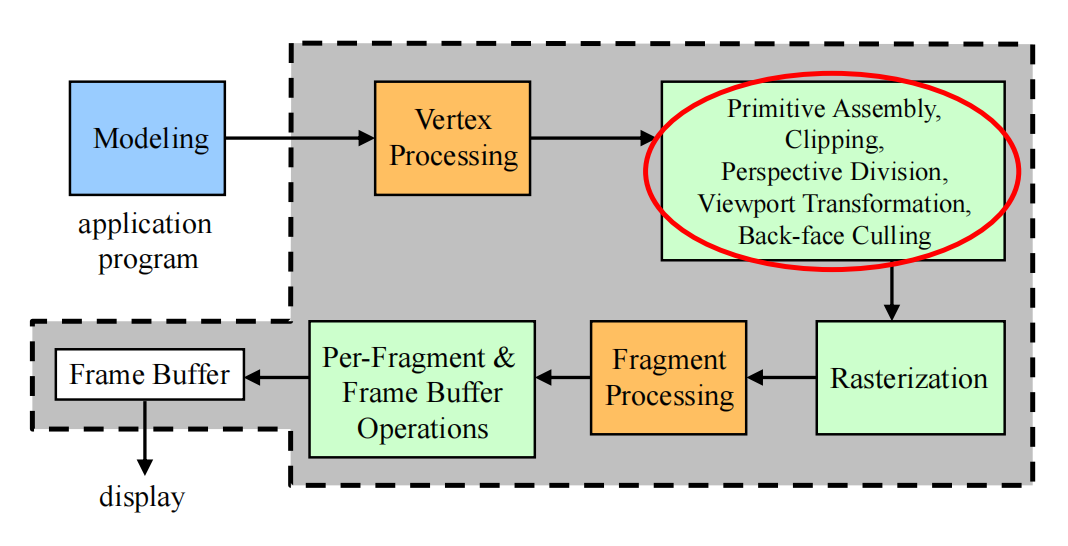
Primitive Assembly, etc.

• Primitive assembly
  • Vertex data is collected into complete primitives
  • Necessary for clipping and back-face culling
• Clipping
• Perspective division (Object Oriented)
  • To normalized device coordinate (NDC) space
• Viewport transformation (Viewer Oriented)
  • To window space
  • Include depth range scaling
• Back-face culling

Rasterization & Fragment Processing

• Attribute values at fragments are computed by interpolating attribute values assigned to vertices
  • Interpolation is performed in window space (2D)

• Each generated fragment is processed to determine the color of the corresponding pixel in the frame buffer
• Fragment color can be modified by texture mapping (纹理映射)
  • Texture access (using interpolated texture coordinates)
    • Access texture map using texture coordinates
  • Texture application
    • Texture color can be combined with the fragment color of the primitive

Per-Fragment Operations

• Fragment is discarded if it is blocked (occluded) by the corresponding pixel already in the frame buffer
  • Z-buffer hidden-surface removal
• Fragment may be blended with the corresponding pixel already in the frame buffer
  • Blending

Let’s talk about something important !!!

Clipping

To clip out primitives that are outside the view volume

Clipping 2D Line Segments

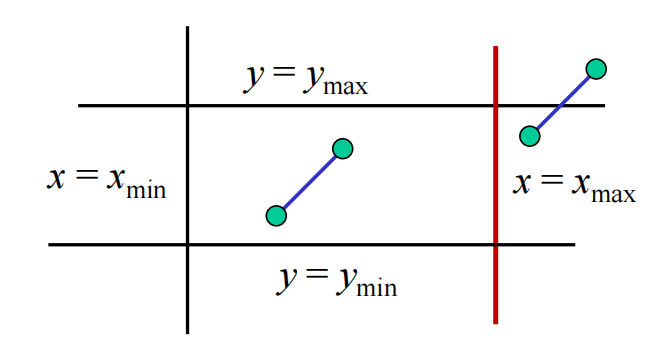
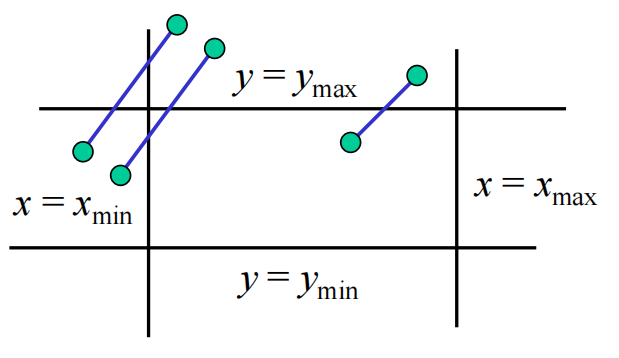
Cohen-Sutherland Algorithm

• Using edge table

	Case 1: Both endpoints inside all four lines Draw (accept) line segment as is Case 2: Both endpoints outside same line Discard (reject) the line segment
	Case 3: One endpoint inside all lines and one outside Must do at least one intersection Case 4: Both outside May have part inside Must do at least one intersection

Using Outcode

E.g. Suppose a line $AB$ with endpoints $A$ and $B$ .

• If $\text{outcode}(A)=\text{outcode}(B)=0$ , accept the segment
• If $\text{outcode}(A)=0$ , $\text{outcode}(B)\not= 0$ ,
  • Compute intersection
  • Location of $1$ in outcode($B$) determines which edge to intersect with
  • If outcode($B$) has two $1$’s, then need to do two intersections
• If $\text{outcode}(A)$ & $\text{outcode}(B) \not= 0$ , reject the segment

• If $\text{outcode}(A)$ & $\text{outcode}(B) = 0$ , but neither of them are $0$ ,

  • Shorten line segment by intersecting with one of sides of window
  • Compute outcode of intersection (new endpoint of shortened line segment)
  • Re-execute algorithm

• When it goes to 3D, we can use 6-bit outcode to represent 6 faces of the window.

Polygon Clipping

Problems of polygon clipping: may generate multiple polygons.

Solution: For concave polygons, use tessellation function(镶嵌函数) in GLU to change it to multiple convex polygons.

• simple way: set axis-aligned bounding box(AABB) for simple calculation.

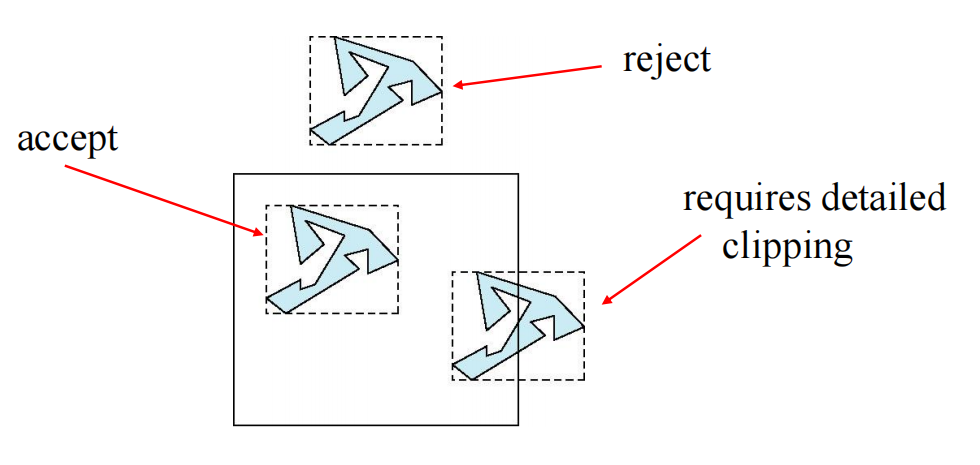
Rasterization

Scan Conversion of Line Segments

Bresenham’s Algorithm

• Key thought: A binary decision problem on how the next pixel lies based on the previous pixel.

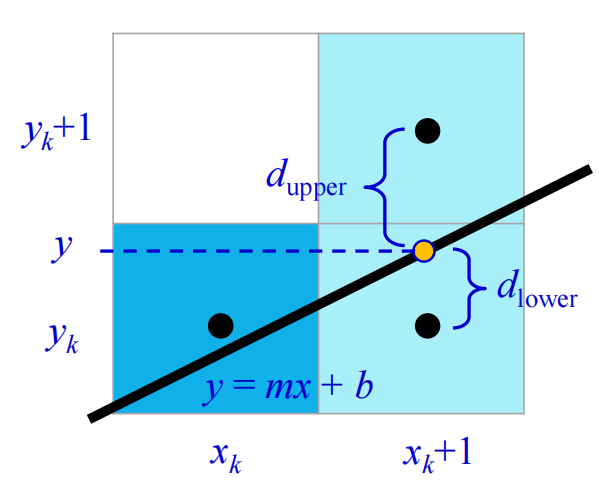
• On the next point: $y=m(x_k + 1) + b$
• $d_\text{lower} = y-y_k$
• $d_\text{upper}=(y_k+1)-y$

$
\begin{align}
p_k&=\Delta x(d_\text{lower} - d_\text{upper}) \\
&=2x_k \Delta y - 2y_k \Delta x + c
\end{align}
$

where $c=2\Delta y + \Delta x (2b - 1)$ is an integer constant .

• If $p_k > 0$ , plot upper pixel

• If $p_k < 0$ , plot lower pixel

• We can incrementally compute $p_{k+1}$ from $p_k$

  • If $p_k > 0$ , $p_{k + 1} = p_k + 2\Delta y – 2\Delta x$
  • If $p_k < 0$, $p_{k + 1} = p_k + 2\Delta y$
  • where $p_0=2\Delta y - \Delta x$

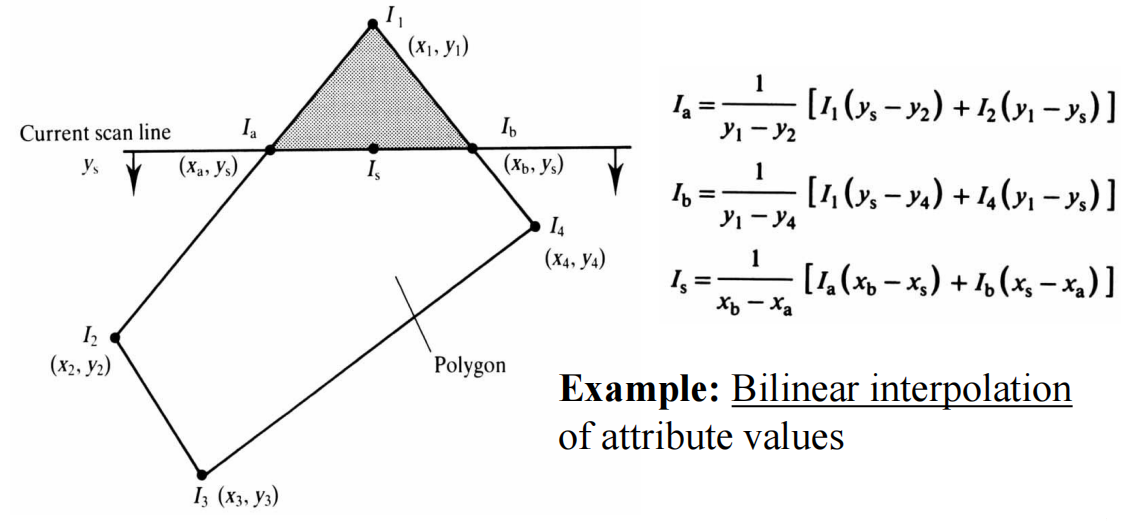
Scan Conversion of Polygons

Scan-Line Fill — Interpolation

• $C_1$ $C_2$ $C_3$ specified by glColor or by vertex shading (lighting computation)
• $C_4$ determined by interpolating between $C_1$ and $C_3$
• $C_5$ determined by interpolating between $C_2$ and $C_3$
• Interpolate between $C_4$ and $C_5$ along span

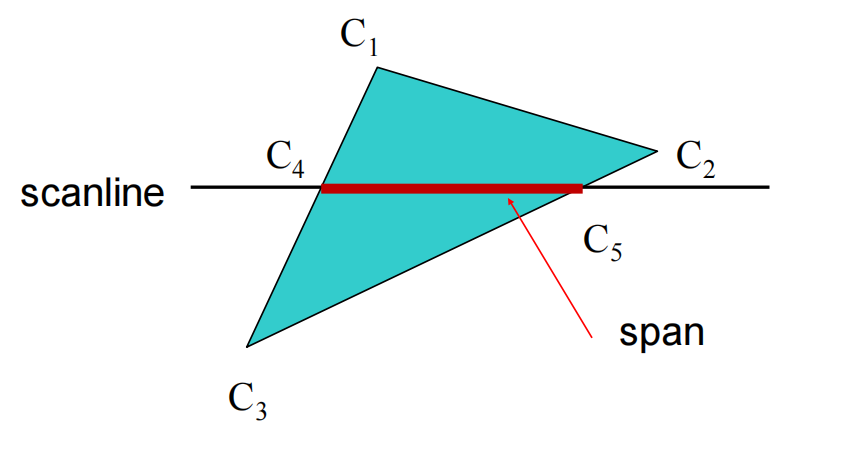
So what we need to do in this algorithm is calculating :

1. points intersact with scan-line (Recall Bresenham’s Algorithm)
2. which polygons lie on this pixel (多边形扫描转换，边表，活动边表)

Hidden-Surface Removal

• Painter’s Algorithm
  • Fill the objects at the back first, then cover with the front objects
• Depth Sorting
  • Need $O(n^2)$ at worst

Back-Face Culling

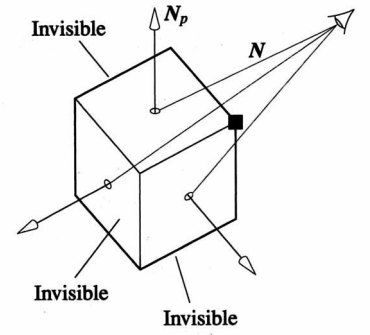
• Polygons is back-facing if $\textbf{N}_p \cdot \textbf{N} <0$
• In OpenGL, we can simply enable culling
  • By default, polygon vertices must be provided in counter clockwise order
  • But may not work correctly for non-convex polygon

Z-Buffer

• Key thought: Exchange time with space
• Use a z-buffer (depth buffer) to store the depth of the closest object at each pixel found so far

Summary

• Viewing this pipeline again:
• Using back-face culling to remove hidden-surface
• Using scan conversion to do rasterization
• Using z-buffer to test the per-fragment
• At the end, output frame buffer.

---

VII. Illumination

Local Reflection vs Global Illumination

• Local reflection
  • Considers relationship between a light source, a single surface point, and a view point
  • No interaction with other objects
• Global illumination
  • Considers all light sources and surfaces
  • Inter-reflections and shadows

Phong Illumination Equation

$
I_{\text{Phong}}=k_a i_a + \sum_{m \in \text{lights}} \left(k_d (\textbf{L}_m \cdot \textbf{N}) i_{m,d} + k_s (\textbf{R}_m \cdot \textbf{V})^{\alpha} i_{m,s} \right)
$

where :

• $k_a$ 表示环境光反射系数，常数
• $k_d$ 表示漫反射系数，常数
• $k_s$ 表示镜面高光反射系数，常数
• $\alpha$ 表示物体材质光滑程度，由材质决定（材质越光滑系数越大），常量
• $\textbf{L}_m$ 表示相对于 $L$ 的反射光线方向
• $\textbf{N}$ 表示该点的法线 [Normal Vector]
• $\textbf{R}_m$ 表示反射光的方向
• $\textbf{V}$ 表示摄像机的方向
• $i_{m,d}$ 表示光源$m$的漫反射反射光照，RGB
• $i_{m,s}$ 表示光源$m$的高光反射光照，RGB
• $i_a$ 表示环境光的光照，RGB
• $I_p$ 表示 $p$ 的总光照，RGB
• $m$ 表示其中一个光源

Sum 中的两项分别对应下图的两步（Diffuse【漫反射】是 $L \cdot N$ ，Specular 【镜面】是 $R \cdot V$），ambient 对应 $k_a \times i_a$ ，表示局部的环境色渲染。

• Diffuse Reflection: Lambert’s Cosine Law
  • diffuse reflection $\propto \cos{\theta} = \textbf{N} \cdot \textbf{L}$

Illumination in OpenGL

• Lighting Computation at Vertex Processing stage.
• Specifying Vertex Normal Vectors
  • Set by glNormal*()
    • glNormal3f(x, y, z)
    • glNormal3fv(p)
  • glEnable(GL_NORMALIZE) allows for auto-normalization at a performance penalty
• Enabling Lighting Computation
  • Shading calculations are enabled by
    • glEnable(GL_LIGHTING)
    • Once lighting is enabled, glColor() is ignored
  • Must enable each light source individually
    • glEnable(GL_LIGHTi) $i = 0, 1, 2, \cdots $
  • Can choose light model parameters
    • glLightModeli(parameter, GL_TRUE)
      • GL_LIGHT_MODEL_LOCAL_VIEWER do not use simplifying distant viewer assumption in calculation
      • GL_LIGHT_MODEL_TWO_SIDED shades both sides of polygons independently
  • An example code of using light:

GLfloat diffuse0[] = {1.0, 0.0, 0.0, 1.0};
GLfloat ambient0[] = {1.0, 0.0, 0.0, 1.0};
GLfloat specular0[] = {1.0, 0.0, 0.0, 1.0};
GLfloat light0_pos[] = {1.0, 2.0, 3,0, 1.0};

glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glLightfv(GL_LIGHT0, GL_POSITION, light0_pos);
glLightfv(GL_LIGHT0, GL_AMBIENT, ambient0);		// def ambient
glLightfv(GL_LIGHT0, GL_DIFFUSE, diffuse0);		// def diffuse
glLightfv(GL_LIGHT0, GL_SPECULAR, specular0);	// def spec

• Or using Global Ambient Light : glLightModelfv(GL_LIGHT_MODEL_AMBIENT, global_ambient)

设置材质和设置光源的参数很像，用 glMaterialfv() 函数，第一个参数改成 GL_FRONT, GL_BACK, GL_FRONT_AND_BACK 表示内外渲染

Shading

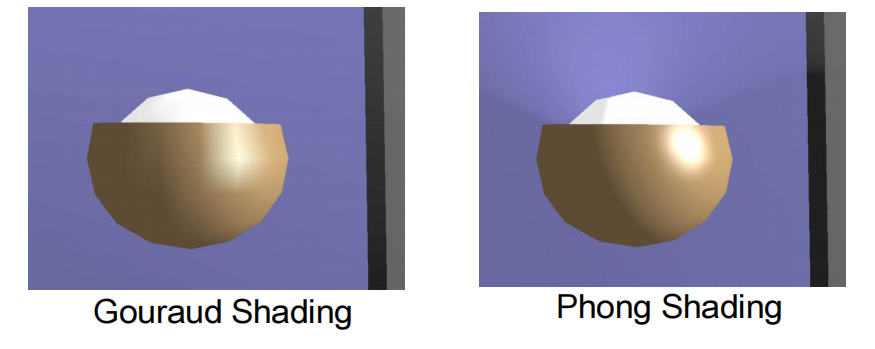
Gouraud Shading vs. Phong Shading

• Flat shading is “bad”
• Gouraud Shading
  1. For each vertex, compute the average normal vector of the polygons that share the vertex
  2. Apply PIE at the vertex using its average normal vector
  3. Smoothly interpolate the computed colors at the vertices of the polygon to the interior of the polygon
• Using Gouraud Shading in OpenGL: glShadeModel(GL_SMOOTH) (No Phong Shading use directly)

• Phong Shading
  1. In Phong Shading, we do not compute the colors of the vertices for interpolation. Instead, for each fragment in the polygon, we interpolate the normal vectors from the vertices
  2. Then, at each fragment, we apply PIE on the interpolated normal vector to compute a color for the fragment

• Differences
  • Highlights are produced more faithfully with Phong shading
  • Gouraud shading produces only “linear interpolation” of colors
  • Gouraud shading may even miss the highlight
• OpenGL does not support Phong Shading
  • But can be done by reprogramming the rendering pipeline using shaders

VIII. Modern OpenGL (Intro)

Example OpenGL Programs: The Modern Way

New Lib

• GLEW
  • The OpenGL Extension Wrangler Library
  • a cross-platform open-source C/C++ extension loading library
  • provides efficient run-time mechanisms for determining which OpenGL extensions are supported on the target platform
  • Automatically initializes the entry points of new OpenGL functions
• GLM
  • OpenGL Mathematics

Examples

注意：由于课程上给出的示例代码过长，这里只总结一些重要部分，不展示示例代码。OpenGL 的相关教程网上不会缺，可以自行获取。

IX. Shading Language

This section is all about coding.

Some basis(Data Type, Data Structure, etc.) is ignored.

Storage Quantifiers

Function Parameter Qualifiers

• GLSL has no concepts of pointer or reference
• Functions are called by value-return

Vertex and Fragment Built-in Variables

• gl_FragCoord contains window relative coordinates $(x, y, z, 1/w)$
  • $z$ is the depth value (after depth range scaling)
  • $w$ is $–z_e$ where $z_e$ is the $z$-coordinate of the fragment in the eye space
• If gl_FragDepth is not written to, gl_FragCoord.z is used as fragment’s depth

• A fragment’s 2D position is the window-relative coordinates of the fragment’s center
  • By default, for the bottom-left-most pixel in the window
    • gl_FragCoord.x == 0.5
    • gl_FragCoord.y == 0.5

Modern OpenGL uses .vert and .frag to describe the vertex and fragment rendering.

// A simple pseudo-code
GLuint ShaderProjObj;
const char vert[] = "exmaple.vert";
const char frag[] = "example.frag";
const GLfloat lightAmbient[] = { 0.0f, 0.0f, 0.0f, 1.0f };

static void MyInit(void) {
  // Create Gouraud Shading shader program object.
  ShaderProjObj = makeShaderProgramFromFiles(vert, frag, NULL);
  // Install Gauraud Shading shader program to the rendering pipeline first.
  glUseProgram(ShaderProjObj);
}

static void MyDrawFunc(void) {
  // Query locations of uniform variables.(exmaple)
  GLint la = glGetUniformLocation(ShaderProjObj, "LightAmbient");
  // Set Uniform variable
  glUniform4fv(la, 1, lightAmbient);
  
  objModel3D->render();
}

---

X. Texture Mapping & Applications

Surface Parameterization

• Defines a mapping between the 3D surfaces and the 2D texture map
  • Defines the mapping $(x_w, y_w, z_w) \leftrightarrow (s,t)$
    • $(x_w, y_w, z_w)$ is the 3D coordinates of surface point
    • $(s, t )$ is the 2D texture coordinates (limited to $[0,1]^2$)
  • Defines which “texel” maps to each surface point
• Difficulty
  • Non-trivial surface topology causes severe distortion of textures (有些不正常的表面拓扑后会产生纹理混乱)

XI. FBO & Shadow Mapping

Framebuffer Objects(FBO)

Multi-Pass Rendering

Def. Render 3D scene multiple times (passes), and “combine” the multiple rendered images to synthesize final frame

• Allows creation of non-displayable framebuffers
• OpenGL can redirect rendering output to FBO
• Each FBO contains a collection of rendering destinations

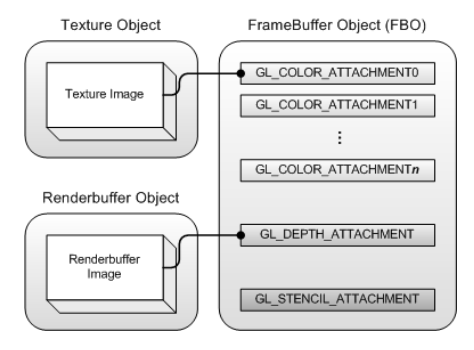
• Two types of framebuffer-attachable images
  • Texture images
    • Render to texture
  • Renderbuffer images
    • Offscreen rendering
• Many color attachment points allow multiple render targets (MRT)
  • Can query the maximum number of color attachment points with GL_MAX_COLOR_ATTACHMENTS (usually 8)

Example

// cpp file
// set up FBO
GLuint fboHandle; // The handle to the FBO

// Generate and bind the framebuffer
glGenFramebuffers(1, &fboHandle);
glBindFramebuffer(GL_FRAMEBUFFER, fboHandle);

// Create first texture object
GLuint renderTexA;
glGenTextures(1, &renderTexA);
glActiveTexture(GL_TEXTURE0); // Use texture unit 0
glBindTexture(GL_TEXTURE_2D, renderTexA);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA8, fboWidth, fboHeight, 0,
  GL_RGBA, GL_UNSIGNED_BYTE, NULL);
// ...

// Attach first texture to FBO
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT2,
  GL_TEXTURE_2D, renderTexA, 0);
  
// ... second texture object as above

// Create the depth buffer
GLuint depthBuf;
glGenRenderbuffers(1, &depthBuf);
glBindRenderbuffer(GL_RENDERBUFFER, depthBuf);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT, 
  fboWidth, fboHeight);

// Bind the depth buffer to the FBO
glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT,
  GL_RENDERBUFFER, depthBuf);

// Set the target for the fragment shader outputs
GLenum drawBufs[] = { GL_COLOR_ATTACHMENT2, GL_COLOR_ATTACHMENT3 };
glDrawBuffers(2, drawBufs);

// Unbind the framebuffer, and revert to default
glBindFramebuffer(GL_FRAMEBUFFER, 0);

// often in other functions
// DRAW TO TEXTURES
// Bind to texture's FBO
glBindFramebuffer(GL_FRAMEBUFFER, fboHandle);

glViewport(0, 0, fboWidth, fboHeight); // Viewport for the texture
glClear(GL_DEPTH_BUFFER_BIT);

// Use glClearBufferfv() to individually clear color buffers
const GLfloat lightGreen[4] = { 0.5f, 1.0f, 0.5f, 1.0f };
const GLfloat lightRed[4] = { 1.0f, 0.5f, 0.5f, 1.0f };
glClearBufferfv(GL_COLOR, 0, lightGreen);
glClearBufferfv(GL_COLOR, 1, lightRed);

// Setup the projection matrix and view matrix
// for the scene to be rendered to the texture here.
// ...

renderTextureScene();

// DRAW FINAL FRAME
// Unbind texture's FBO (back to default FB)
glBindFramebuffer(GL_FRAMEBUFFER, 0);
glViewport(0, 0, winWidth, winHeight); // Viewport for main window
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

// Setup the projection matrix and view matrix.
// ...
renderScene();

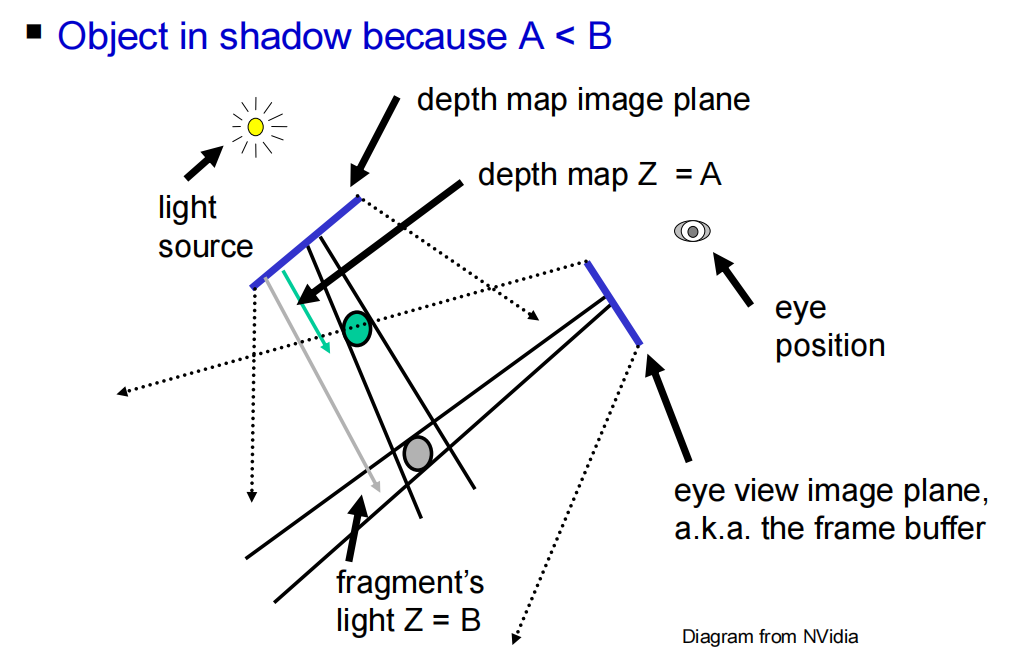
Shadow Mapping

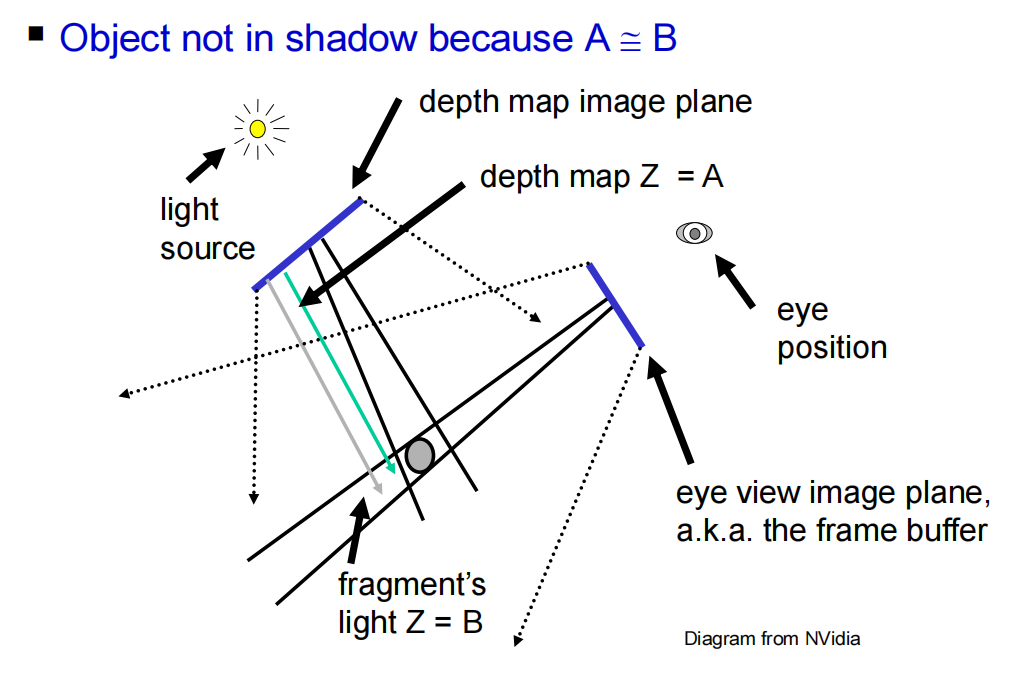Algorithm Overview

1. Render the scene using the light source as viewpoint
2. Save the depth buffer (a.k.a. shadow map)
3. Clear the framebuffer
4. Render the scene from camera’s viewpoint
   • For each fragment, transform it to the “light space” and compare its “light space” $z$ value with the corresponding $z$ value in the shadow map
     • If “light space” z value is larger, the fragment is in shadow and it is lit with only ambient light
     • Otherwise, the fragment is not in shadow and is fully lit

Shadow Map Coordinates

• Any 3D point in the view frustum(视图) of the light source must be transformed to the shadow map coordinates $[s, t, p]$ where $s$, $t$, $p$ are in the range $[0,1]$
• Given a 3D point $p_M$ in modeling coordinates, its shadow map coordinates $p_L$ is

$
p_L=B \cdot P_L \cdot V_L \cdot M \cdot p_M
$

• $M$ is the modeling matrix
• $V_L$ is the light’s view transformation matrix
• $P_L$ is the light’s projection matrix
• and $B=\left[ \begin{array} \\
  0.5&0&0&0.5 \\
  0&0.5&0&0.5 \\
  0&0&0.5&0.5 \\
  0&0&0&1 \\
  \end{array}\right]$

Issues

• shadow acnes(失真)
  • Sol 1: Subtract a tolerance value from ShadowCoord.z in the fragment shader before the depth comparison
  • Sol 2: “Offset” the scene backwards when generating the shadow map from the light source
    • Use OpenGL function glPolygonOffset()
• Obvious jaggies(锯齿)
  • Percentage Closer Filtering (PCF)

// before using PCF
void shadeWithShadow()
{
  vec3 ambient = ...; // ambient
  vec3 diffSpec = ...; // diffuse and specular
  
  // Do the shadow-map lookup
  float shadow = textureProj(ShadowMap, ShadowCoord);
  
  // If the fragment is in shadow, use ambient light only.
  FragColor = vec4(diffSpec * shadow + ambient, 1.0);
}

// after using PCF
void shadeWithShadow()
{
  vec3 ambient = ...; // ambient
  vec3 diffSpec = ...; // diffuse and specular
  
  // The sum of the comparisons with nearby texels
  float sum = 0.0;
  
  // Sum contributions from texels around ShadowCoord
  sum += textureProjOffset(ShadowMap, ShadowCoord, ivec2(-1,-1));
  sum += textureProjOffset(ShadowMap, ShadowCoord, ivec2(-1,1));
  sum += textureProjOffset(ShadowMap, ShadowCoord, ivec2(1,1));
  sum += textureProjOffset(ShadowMap, ShadowCoord, ivec2(1,-1));
  float shadow = sum * 0.25;
  
  FragColor = vec4(diffSpec * shadow + ambient, 1.0);
}

XII. Image Processing

XIII. Ray Tracing

Basic Ray Casting

For every pixel
  Construct a ray from the eye
  For every object in the scene
    Find intersection with the ray 
    Keep if closest
  Shade depending on light and normal vector(using Phong reflection)

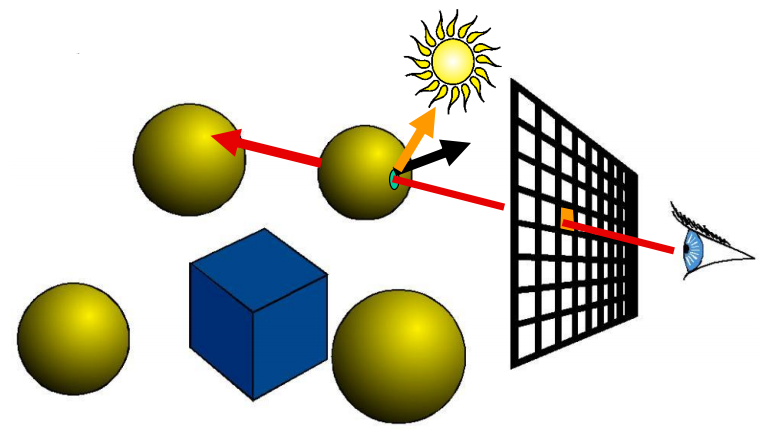
Rasterization vs. Ray Casting

• Rasterization
  • Given a primitive in 3D space, determine which pixels are covered by the primitive
• Ray Casting
  • At each pixel, determine which primitive covers it

Ray Tracing

• From the closest intersection point, secondary rays are shot out
  • Reflection ray
  • Refraction ray
  • Shadow rays

Whitted-style(Recursive) Ray Tracing

$
\begin{align}
&\textbf{I}= \textbf{I}_{\text{local}}+k_{\text{rg}} \textbf{I}_{\text{reflected}}+k_{\text{tg}} \textbf{I}_{\text{transmitted}} \\
\text{where }&\textbf{I}_{\text{local}}= \textbf{I}_{a}k_a+ \color{red}k_{\text{shadow}}\color{black}\textbf{I}_{\text{source}}\left[ k_d(\textbf{N} \cdot \textbf{L}) + k_r (\textbf{R} \cdot \textbf{V})^n + k_t (\textbf{T} \cdot \textbf{V})^m \right]
\end{align}
$

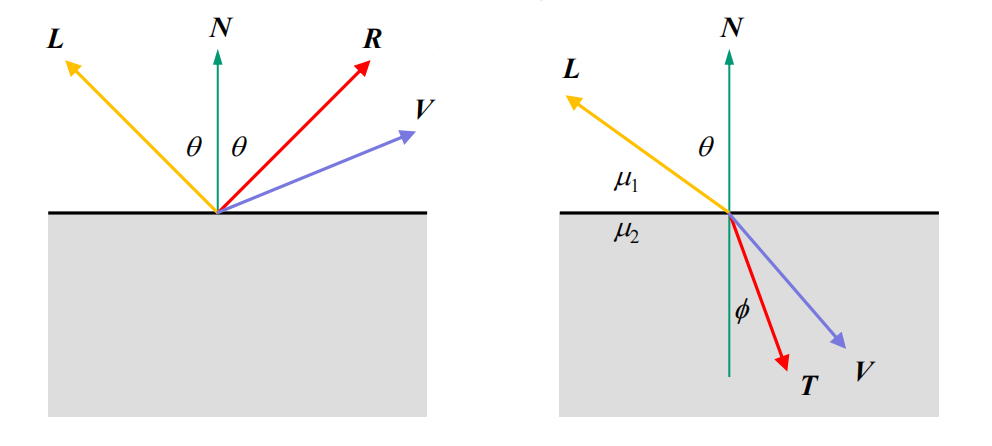
• So if the material is opaque, the $k_t (\textbf{T} \cdot \textbf{V})^m$ can be omitted.
• Also consider Shadow Rays.

Scene Description

• Camera view & image resolution
  • Camera position and orientation in world coordinate frame
    • Similar to gluLookAt()
  • Field of view
    • Similar to gluPerspective(), but no need near & far plane
  • Image resolution
    • Number of pixels in each dimension
• Each point light source
  • Position
  • Brightness and color ($\text{I}_{source}$)
  • A global ambient ($\text{I}_{a}$)
  • Spotlight is also possible
• Each object surface material
  • $k$ (each is a RGB vector)
  • $n$, $m$
  • Refractive index $\mu$ if $k_{tg} \not= 0$ or $k_{t} \not= 0$
• Objects
  • Implicit representations (e.g. plane, sphere, quadrics)
  • Polygon
  • Parametric (e.g. bicubic Bezier patches)
  • Volumetric

Q: When to stop recursion?

• When the surface is totally diffuse (and opaque)
• When reflected/refracted ray hits nothing
• When maximum recursion depth is reached
• When the contribution of the reflected/refracted ray to the color at the top level is too small
  • $(k_{rg1} | k_{tg1}) \times … \times (k_{rg(n−1)} | k_{tg(n−1)}) < \text{threshold}$

Appendices (Reference)

If you want to search the reference pages of OpenGL Programming on C++ , or use real-time 3D rendering in other field using OpenGL API, please refer to the OpenGL® 4.5 Reference Pages .

If you are just interesting in shader rendering (like only do fragment shaders), you can go to shadertoy to take a look at others’ work or create your own.

One of the contributor of “shadertoy”, Inigo Quilez, has published a tutorial of the skills of shadertoy, and you can learn it here → https://iquilezles.org/articles/